Bounding the QCD Equation of State with the Lattice

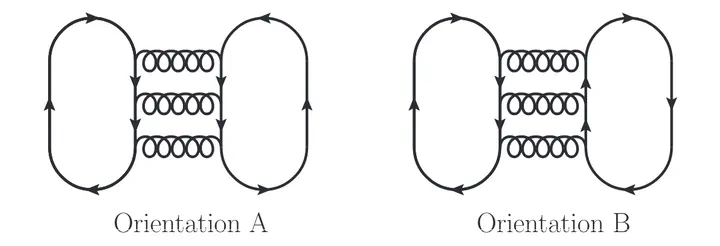
The equation of state of QCD matter at high densities is relevant for neutron star structure and for neutron star mergers and has been a focus of recent work. We show how lattice QCD simulations, free of sign problems, can provide an upper bound on the pressure as a function of quark chemical potentials. We show that at large chemical potentials this bound should become quite sharp; the difference between the upper bound on the pressure $\$P\_\backslash mathrm\{PQ\}\$$ and the true pressure $\$P\$$ is of order $\$P\_\backslash mathrm\{PQ\}-P\; =\; O(\backslash alpha\_s^3\; P)\$$. The corrections arise from a single Feynman diagram; its calculation would render remaining corrections $\$O(\backslash alpha\_s^4\; P)\$$.

JHEP 12 (2023) 133